Dualsystem
gebräuchliche Basis von Zählmaschinen, abgeleitet von den beiden möglichen Schaltzuständen: aus, ein.
auch als Binärsystem bezeichnet

Tridynalsystem
Zahlensystem zur Basis 3, wird selten verwendet und noch seltener benannt.

Quadralsystem
  Zahlensystem zur Basis 4, nicht sehr gebräuchlich, aber geeignet, Dualzahlen halb so lang darzustellen.

Pentalsystem
Zahlensystem zur Basis 5

Hexalsystem
Zahlensystem zur Basis 6

Heptalsystem
Zahlensystem zur Basis 7

Oktalsystem
Zahlensystem zur Basis 8

Nonalsystem
Zahlensystem zur Basis 9, kompatibel zum Tridynalsystem

Dezimalsystem
Zahlensystem mit der Basis 10, orientiert sich offensichtlich an zwei Händen mit je 5 Fingern (2·5=10).
Das gebräuchlichste Zahlensystem.

Hexadezimalsystem
Zahlensystem zur Basis 16 
Zahlenwerte von zehn bis fünfzehn werden durch Buchstaben (A bis F) wiedergegeben.

Basis: 2

Jede Stelle kann als 2er-Potenz dargestellt werden:

101₂ = 1x2² + 0x2¹ + 1x2⁰

1001₂ = 8 + 0 + 0 + 1 = 9₁₀

1010₂ = 8 + 0 + 2 + 0 = 10₁₀

1100₂ = 8 + 4 + 0 + 0 = 12₁₀

1011₂ = 8 + 0 + 2 + 1 = 11₁₀

Die Addition

           25₁₀                                                                                1            1            0            0          1

+         49 ₁₀                                                                     1           1            0            0            0          1

=         74₁₀                                                       1            0             0            1            0            1         0

1. Alle Zahlen stehen in der Reihenfolge: hoch -> niedrig
2. Hauptsymbole I (1), X (10), C (100), M (1000) dürfen max, 3 mal hintereinander stehen
3. Nebensymbole V (5), L (50), D (500) dürfen nur 1 mal verwendet werden & nicht vor einem höherwertigen Symbol stehen
4. Vor einem Symbol steht höchstens das nächstkleinere Symbol

BSP:      2016 = MMXVI        (1000 + 1000 + 10 + 5 + 1)

                900 = CX                (100 - 10)

                  49 = XLIX              ((50 - 10) + (10 - 1))

                  99 = XCIX              ((100 - 10) + (10 - 1))

               999 = CMXCIX         ((1000-100) + (100 - 10) + (10 - 1))

             1997 = MCMXCVII   ( 000 + (1000-100) + (100 - 10) + 5 + 2)

Basis: 20

Zahlen über 19 werden in einer höheren "Ebene" dargestellt, also über der ersten Zahl. Die nächsthöhere Ebene ist dabei immer das 20-fache der vorherigen Grundzahl, also:

1, 20, 400, 8000, 160000,usw...

Einige Rechnungen:

(20 x 1 =) 20 + (1 x 5 =) 5 Total = 25    25    (20 x 1 =) 20 + (1 x 9 =) 9 Total = 29    29    (20 x 1 =) 20 + (1 x 17 =) 17 Total = 37    37    (20 x 4 =) 80 + (1 x 14 =) 14 Total = 94    94    (20 x 17 =) 340 + (1 x 3 =) 3 Total = 343    343

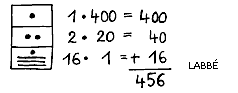
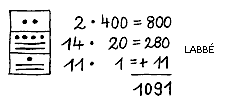
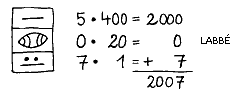
Erkennen, ob eine Mayazahl gerade ist:

Gerade Anzahl Punkte + Gerade Anzahl Linien = Gerade

Ungerade Anzahl Punkte + Ungerade Anzahl Linien = Gerade

Basis: 60

Hat wie mehrere stellen. Nach 59 beginnt man mit den Zeichen wieder von vorne, diesmal bedeutet die 1 aber 60 und es wird waagrecht nebeneinander statt übereinander geschrieben.