Eigenschaften von Zahlen
Teilbarkeitsregeln natürlicher Zahlen
- 2, wenn die letzte Ziffer 0,2,4,6 oder 8 ist (also letzte Ziffer durch 2 teilbar, dann ja)
- 5, wenn letzte Ziffer 5 oder 0 ist (also letzte Ziffer durch 5 teilbar, dann ja)
- 10, wenn letzte Ziffer eine 0 ist
- 3, wenn Quersumme durch 3 teilbar
- 9, wenn Quersumme durch 9 Teilbar
- 4, wenn die letzten 2 Ziffern eine Zahl ergeben, welche durch 4 teilbar ist, und wenn 00 am Schluss
- 25, wenn die letzten 2 Ziffern durch 25 teilbar sind und wenn 00
- 8, wenn due letzten 3 Ziffern durch 8 teilbar sind
- 125, wenn die letzten 3 Ziffern durch 125 teilbar sind
Primfaktorzerlegung
Man zerlegt eine Zahl so lange in Produkte aus Primzahlen, bis sie nicht weiter teilbar ist. Man fängt dabei bei der kleinsten Primzahl, also 2, an und das so lange, bis diese Zahl nicht mehr
geht, worauf man zur nächst grösseren wechselt. Dies tut man so lange, bis am Schluss eine Primzahl übrig bleibt und wir eine Multiplikation nur als Primzahlen haben.
Zuerst mal alle Primzahlen bis 100:
Beispiele:
Primfaktorzerlegung von 48.
Zuerst testet man 48 auf Teilbarkeit durch 2. 48 ist durch 2 teilbar, und 48=2*24. Auch 24 ist durch 2 teilbar; es gilt: 24=2*12; also 48=2*2*12, und weiter 48=2*2*2*6=2*2*2*2*3. Da 3 eine
Primzahl ist, kann man nun aufhören.
Anderes Beispiel: Primfaktorzerlegung von 18.
Es gilt: 18=2*9. 9 ist nicht durch 2 teilbar; also testet man mit der nächsten Primzahl weiter: 9 ist durch 3 teilbar, und 9=3*3, also 18=2*3*3.
Das kleinste gemeinsame Vielfache (kgV)
Es gibt verschiedene Methoden, den kgV zu bestimmen, wir tun es jetzt aber mit der Primfaktorzerlegung, da dies vorher ja gerade erklärt ist.
Als erstes bilden wir also die Primfaktorenzerlegung der beiden Zahlen.
Beispiel: 336 und 198
336 = 2*2*2*2*3*7
198 = 2*3*3*11
Nun schauen wir, in welcher der beiden Zahlen jeweils die grössere Anzahl einer Primzahl vorkommt und nehmen diese dann in die Endrechnung:
2er: von 336 -> 2*2*2*2
3er: von 198 -> 3*3
7er: von 336 -> 7
11er: von 198 -> 11
Das kgV von 336 und 198 ist also: 2*2*2*2*3*3*7*11 = 11088
Der grösste gemeinsame Teiler (ggT)
Um den ggT von zwei Zahlen zu bestimmen, bestimmt man zuerst die Primfaktorzerlegungen der beiden Zahlen. Dann schauen wir, welche Faktoren in beiden Zerlegungen vorkommen. Diese Faktoren multiplizieren wir und erhalten so den ggT. Also in unserem Beispiel wurde das so gehen:
56 = 2·2·2·7
84 = 2·2·3·7
Die dicken Zahlen kommen in beiden Faktorzerlegungen vor. Wir multiplizieren sie und erhalten somit den ggT:
ggT von 56 und 84 = 2·2·7 = 28
Zahlenmengen
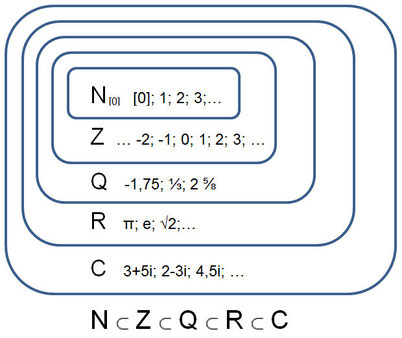
Natürliche Zahlen
Symbol: N oder N0
positive ganze Zahlen
Ganze Zahlen
Symbol: Z oder Z0
Alle negativen ganzen Zahlen auch dazu
.... -3, -2, -1, 0, 1, 2, 3,...
Rationale Zahlen
Symbol: Q oder Q0
Alle Bruchmengen (Quotient zweier ganzer Zahlen) dazu
Reelle Zahlen
Symbol: R oder R0
alle rationalen und irrationalen Zahlen dazu: unendliche, nicht periodische und demzufolge nicht als Bruch darstellbare Zahlen
Vollkommene Zahlen
Zahl a ist vollkommen, wenn gilt: a = die Summe all ihrer Teiler
(die Zahl 1 wird als Teiler gezählt, die Zahl a selbst aber nicht)
6 ist eine vollkommene Zahl, da 1+2+3 = 6
Befreundete Zahlen
Die Zahlen a und b sind befreundet, wenn die Teilersumme von a gleich b ist und umgekehrt.
Beispiel: 220 und 284 sind "befreundet".
Teilersumme von 220 = 1+2+4+5+10+11+20+22+44+55+110 = 284
Teilersumme von 284 = 1+2+4+71+142 = 220
π
Die Kreiszahl π gibt das Verhältnis des Masszahlen von Umfang und Durchmesser eines Kreises an.
Diese Zahl ist irrational, also nicht als Bruch zweier Zahlen darstellbar.
